Magnitude of Numbers

COMMON DENOMINATOR

• Rational numbers arise from the attempt to measure all quantities with a common unit of measure.

The pursuit of infinity begins with an examination of the idea of number, or quantity. Numbers originally were tools used to quantify groups of objects or to measure real things, such as the length of a pole or the weight of a piece of cheese. Measuring something requires some fundamental unit that can be used as a basis of comparison. Some things, such as rope or time, can be measured, or quantified, using a variety of units. In measuring a length of rope, for example, we might express the result as either "5 feet" or "60 inches." The length of time from one Monday to the next Monday is commonly called a "week, " but we could just as easily—and correctly—call it seven "days, " 168 "hours, " 10, 080 "minutes, " or 604, 800 "seconds." These number expressions all represent the same length of time and, thus, are interchangeable. Converting any one of these equivalent values into another simply requires multiplying or dividing by some whole number. For example, 10, 080 minutes is 168 hours times 60. In fact, every one of the above measurements could be converted into seconds by multiplying by appropriate whole number values.

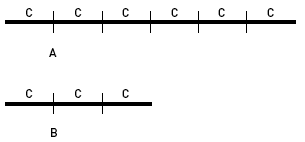
Now, we can take any two quantities and ask a similar question: can we find a common unit of measurement that fits a whole number of times into both? Take 8 and 6, for example. This is straightforward; both 8 and 6 are whole numbers, so we can use whole units to measure them both. What about and ? Here, each of the quantities uses different base units, namely halves and eighths, and comparing them would make little sense, because they are different things. We can find a common unit of comparison, however, by recognizing that is the same as .

So, we found a common denominator of 8, which implies that both of the fractions could be expressed as multiples of the same unit, "one eighth." In some sense, we have redefined our basic unit of measurement, or fundamental piece, to be of the original piece, thereby transforming the original fractions into easily-compared multiples of the same fundamental unit.

If two numbers can be expressed as whole-number multiples of some common unit, of whatever size, they are in some sense "co-measurable" in that we can measure both using the same ruler. The proper mathematical term for "comeasurable" is "commensurable." One way to think about this is that two lengths are commensurable if there is a basic unit of measure that fits into both of them a whole number of times. If we were to cut some length of rope into two pieces of lengths a and b, there would be some third length, c, such that a = mc and b = nc. In other words, these two numbers could be expressed as multiples of some common unit.

Using a little algebra, we can confirm that the ratio of magnitudes of our two commensurable quantities is equal to a ratio of whole numbers:

Canceling the common factor of c yields the equation:

Numbers that can be expressed as ratios of two whole numbers are called rational numbers. This idea of "creating" numbers that may not relate to any observable value in the real world is fairly modern. Although today we are comfortable speaking of a number such as as a concept that "exists" in its own right, the ancient Greeks generally took care to phrase things only in terms of geometric quantities—those that exist in the physical world. For instance, they might have spoken of two lengths of rope, one that could be described as 13 measures of a certain unit, and the other 25 units of that same measure, but they would not necessarily speak of the shorter length being of the other.

On the other hand, today we are comfortable saying, for example, that a length of string is of an inch long. In doing so, we are saying that it is commensurable with a piece of string one inch long, the fundamental unit of comparison being.

The modern and ancient views of rational numbers are intimately linked, but it is important to remember that the Greeks thought of commensurability in terms of whole units. The Pythagoreans, the followers of Pythagoras of Samos in 6th century BC Greece, held sacred the idea that the first principle underlying everything is "arithmos, " the intrinsic properties of whole numbers and their ratios. It is certainly a tidy idea that whole numbers, or ratios of them, are all that is required to describe the world mathematically. It is thought that this belief had origins in both the study of figurate numbers and the recognition that strings or hammers of commensurable length sounded harmonious when played or struck together.

THE EVER-EXPANDING DECIMAL

• Rational numbers can be expressed as decimals that repeat to infinity.

In any ratio of two whole numbers, expressed as a fraction, we can interpret the first (top) number to be the "counter, " or numerator—that which indicates how many pieces—and the second (bottom) number to be the "namer, " or denominator—that which indicates the size of each piece.

In modern arithmetic, we use a base-10 system to count, or evaluate, things. Large quantities are generally represented in terms of ones, tens, hundreds and the like, whereas small quantities are more easily represented in terms of tenths, hundredths, thousandths, and so on. Although the Greeks did not use a base-10, or decimal, number system, it is illuminating to see how rational numbers behave when expressed as decimals.