Debye screening length

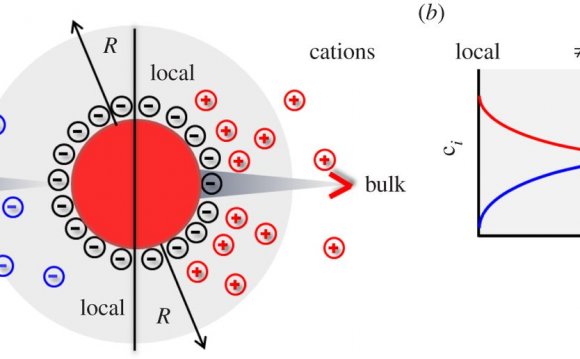
In the previous reading on Screening of electrical interactions in salt solution, we found that the charge on a a DNA molecule in a salt solution experiences a screening effect as a result of the salt ions clustering near the DNA. As a result, the electric field produced by a charged biological macromolecule should be different than it would produce in a vacuum.

To make this quantitative we would like to know two things:

• How large is the volume occupied by the positively charged ions that neutralize the negatively charged DNA — the “screening cloud”? Put differently, how far away from the DNA do we have to go before the electric field will drop essentially to zero?
• What is the mathematical function describing how the electric field and the electric potential depend on distance?

Let’s begin by reasoning about the physical parameters that determine the size of the screening cloud. Specifically, let’s model the screening cloud as extending a distance λD, known as the “Debye length, ” away from the DNA at every point. (The Greek letter λ is named “lambda” and corresponds to our letter “L” so it is commonly used in science to denote lengths.) Inside the cloud there are many more positive ions than negative; outside the cloud there are equal concentrations of positive and negative ions. What determines this size λD?

• If temperature increases, the effects of entropy and temperature also increase. We'd expect the screening cloud to spread out due to the increased molecular motion. Therefore, λD should increase as T increases.
• If the undisturbed concentration c0 of salt ions increases, then the number of ions that have to be moved away from an even distribution in order to form the screening cloud is a smaller fraction of the total. Therefore, the fractional change in concentration required to screen the DNA is smaller. This means that the entropic cost of forming the screening cloud decreases as the salt concentration increases. Therefore, λD should decrease as c0 increases.
• If the charge of the individual positive ions increases, fewer of them are needed to screen the DNA and again the entropic cost of forming the screening cloud is less. Therefore λD should decrease as Ze, the charge of one of the positive ions, increases.

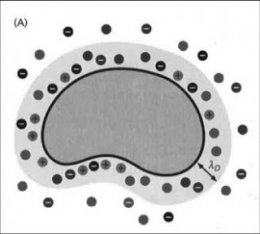
The mathematical expression for the size of the screening cloud λD is determined by solving differential equations to find the arrangement that balances electric potential energy and entropy. We won’t do that in this class, but we’ll make use of the result.