![Fission reactors[edit]](http://www.plasma-physics.com//img/nuclear_fission_wikipedia_the_free.jpg)
 Nuclear Reactions Fission And Fusion
Nuclear Reactions Fission And Fusion
Construct and complete nuclear reaction equations
Artificial transmutation is the changing or manipulation of a nucleus artificially. The nuclear reaction equation below is an example of artificial transmutation:
Nitrogen is bombarded with alpha particles (helium) resulting in the creation of oxygen and hydrogen. The alpha particle is absorbed by the nitrogen and a proton (hydrogen w/o an electron) is released. This happened because someone set it up, thus its artificial, and the nitrogen transmutated into oxygen.
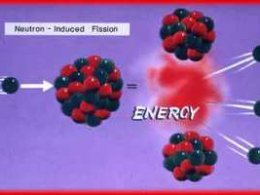
Another example of a nuclear reaction is the Fission of Uranium-235 by a slow (thermal) neutron:
Uranium-235 absorbs a neutron becomes Uranium-236 which is very unstable and quickly breaks down into Strontium and Xeon. This is one of several possible fission reacts, all Uranium fission uses U-235 to create U-236, however the products are not always the same (as with everything quantum-like there are probabilities dictating the outcome).
It is important to note that there are three “conservation laws” that apply to nuclear reactions:
- The number of nucleons in a nuclear reaction is conserved.
- The charge is conserved, or the sum of the charges on the left is equal to the sum of the charges on the right.
- The mass energy is conserved, more on that later…
Solve problems involving mass defect and binding energies
The proton and neutron have very nearly equal mass, albeit very small, approximately . This is not a very convenient number, so a new unit was defined the atomic mass unit, or as the IB likes to call it the unified mass unit, u. One unified mass unit is defined as one-twelfth the mass of a carbon-12 atom. Carbon-12 has 6 protons and 6 neutrons.
(1)\begin{align} 1 u = \frac{mass \: of \: one \: carbon \: 12 \: atom}{12} \end{align}
This is call an atomic mass unit by Americans, I guess British or the IB likes to be different, who cares. A unified mass unit (u) is defined to be the mass of exactly one-twelfth of a carbon-12 atom. That works out to be:
(2)\begin{align} 1u = 1.66 \times 10^{-27} kg \end{align}
Since the neutron and proton have approximately the same mass, a proton and neutron have approximately mass’s of approximately 1u.
In the IB formula book:
| Particle | Mass (u) |
| Electron (me) | 0.000549 |
| Proton (mp) | 1.007277 |
| Neutron (mn) | 1.008665 |
| Helium Atom | 4.002602 |
If the math is done it can be seen that the helium atom weighs less than the mass of two protons and two neutrons! The same can be found with Oxygen that weighs 15.994915 u, if fact it can be found for all atoms. The difference between the mass of an atom and the sum of an atom’s parts is called the mass defect.
The mass defect can be explained by Einstein’s mass-energy equivalence:
(3)\begin{equation} E = mc^2 \end{equation}
If you slam to small nuclei into each other and create a bigger atom (but with less mass) then energy is released. The loss of mass is equal to the energy released. For example:
It will take energy to break the new nucleus apart, the energy required to break up a nucleus into in neutron and protons is called the binding energy. In the reaction shown above the energy required to reverse the reaction (break up the helium into hydrogen) is equal to the energy released.
The binding energy of an atom can be approximated summing the mass of the individual neutrons and the mass of the individual protons subtracting the mass of the atom and multiplying by the speed of light squared:
(4)\begin{align} E = \left [ N \cdot m_n + Z \cdot m_p - mass \: of \: atom \right ] c^2 \end{align}
Where N is the number of neutrons, mn the mass of a neutron (u), Z is the number and protons, mp is the mass of a proton (u) and c is the speed of light in MeV u-1.
YOU MIGHT ALSO LIKE