 The step from molar concentrations (analytical data) to activities (that enter law-of-mass-action calculations) requires the calculation of activity coefficients γi. For this task several approaches are available, whereas each activity model has its own range of validity defined by the ionic strength I as shown here:
The step from molar concentrations (analytical data) to activities (that enter law-of-mass-action calculations) requires the calculation of activity coefficients γi. For this task several approaches are available, whereas each activity model has its own range of validity defined by the ionic strength I as shown here:
| Model | Equation | Validity |
| (1) | Debye-Hückel | I < 10-2.3 M |
| (2) | Extended Debye-Hückel | I < 0.1 M |
| (3) | Davies | I ≤ 0.5 M |
| (4) | Truesdell-Jones (WATEQ Debye-Hückel) | I < 1 M |
Here, zi is the valence of ion i. All quantities carrying the subscript i are ion-specific parameters (ai, ai0 and bi). On the other hand, the parameters A and B depend on temperature T and the dielectric constant ε:
| (5a) | A = 1.82 ∙ 106 (εT)-3/2 |
| (5b) | B = 50.3 (εT)-1/2 |
For standard conditions (water at 25°C) we get
| (6a) | A = 0.5085 M-1/2 |
| (6b) | B = 3.281 M-1/2 nm-1 |
Please note the length unit: 1 nm = 10-9 m = 10 Ångström.
The relationship between the activity models becomes most evident when they are all traced back to the simple Debye-Hückel formula in Eq.(1). Denoting the “Debye-Hückel building block” by lg γi0 the equations above can be rewritten as:
| (1b) | ||
| (2b) | ||
| (3b) | ||
| (4b) | Truesdell-Jones | 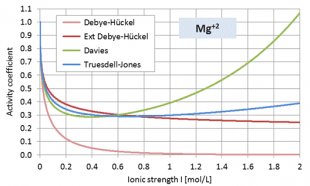 I < 1 M I < 1 M |
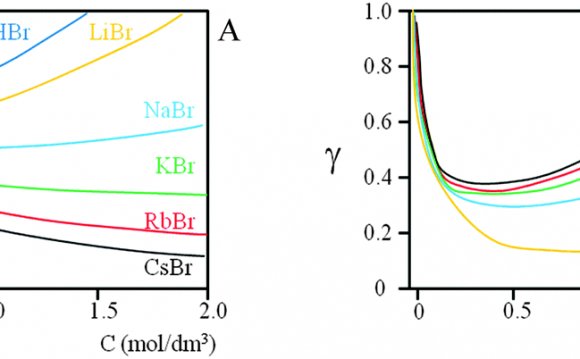
The activity coefficients decrease steadily when the ionic strength I rises. However, both the Davies and Truesdell-Jones equations obey an additive term that causes a renewed increase when I approaches 1 mol/L – see diagrams below.
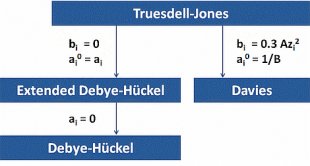
Model Hierarchy. The empirical model of Tuesdell-Jones in Eq.(4) and Eq.(4b), with its two ion-specific parameters ai0 and bi, represents the most general approach. By specifying and/or ignoring these two parameters we obtain the other three activity models.
Extended Debye-Hückel Equation
Due to the narrow validity range of the Debye-Hückel formula in Eq.(1), this approach was extended in Eq.(2) by an additional term in the denominator containing the parameters B and ai. The extended formula considers the fact that the central ion has a finite radius (rather than a point charge). The parameter ai represents the effective size of the corresponding ion, for example:
| a = 0.9 nm | for | H+, Fe+3, Al+3 |
| a = 0.8 nm | Mg+2 | |
| a = 0.6 nm | Ca+2, Fe+2 | |
| a = 0.4 nm | Na+, HCO3-, SO4-2 | |
| a = 0.3 nm | K+, NH4+, OH-, Cl-, NO3- |
Note. The ion size parameter ai is an empirical fit parameter; it is larger than the ionic radius because it includes some aspect of hydrated shell.
Davies Equation
The Davies formula in Eq.(3) is an empirical approach which differs in two respects from the extended Debye-Hückel Eq.(2):
- it get rid of the ion-size parameter ai (which is not well known for complex ions)
- the additional term 0.3⋅I, which is linear in the ionic strength I
YOU MIGHT ALSO LIKE