Magnitude definition Math

In the introduction to vectors, we discussed vectors without reference to any coordinate system. By working with just the geometric definition of the magnitude and direction of vectors, we were able to define operations such as addition, subtraction, and multiplication by scalars. We also discussed the properties of these operation.

Often a coordinate system is helpful because it can be easier to manipulate the coordinates of a vector rather than manipulating its magnitude and direction directly. When we express a vector in a coordinate system, we identify a vector with a list of numbers, called coordinates or components, that specify the geometry of the vector in terms of the coordinate system. Here we will discuss the standard Cartesian coordinate systems and .

Vectors in the plane

We assume that you are familiar with the standard $(x, y)$ Cartesian coordinate system in the plane. Each point $\vc{p}$ in the plane is identified with its $x$ and $y$ components: $\vc{p} = (p_1, p_2)$.

To determine the coordinates of a vector $\vc{a}$ in the plane, the first step is to translate the vector so that its tail is at the origin of the coordinate system. Then, the head of the vector will be at some point $(a_1, a_2)$ in the plane. We call $(a_1, a_2)$ the coordinates or the components of the vector $\vc{a}$. We often write $\vc{a} \in \R^2$ to denote that it can be described by two real coordinates.

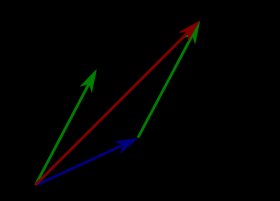
The sum of two vectors. The sum $\vc{a}+\vc{b}$ of the vector $\vc{a}$ (blue arrow) and the vector $\vc{b}$ (red arrow) is shown by the green arrow. As vectors are independent of their starting position, both blue arrows represent the same vector $\vc{a}$ and both red arrows represent the same vector $\vc{b}$. The sum $\vc{a}+\vc{b}$ can be formed by placing the tail of the vector $\vc{b}$ at the head of the vector $\vc{a}$. Equivalently, it can be formed by placing the tail of the vector $\vc{a}$ at the head of the vector $\vc{b}$. Both constructions together form a parallelogram, with the sum $\vc{a}+\vc{b}$ being a diagonal. (For this reason, the commutative law $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ is sometimes called the parallelogram law.) You can change $\vc{a}$ and $\vc{b}$ by dragging the yellow points.

You may have noticed that we use the same notation to denote a point and to denote a vector. We don't tend to emphasize any distinction between a point and a vector. You can think of a point as being represented by a vector whose tail is fixed at the origin. You'll have to figure out by context whether or not we are thinking of a vector as having its tail fixed at the origin.

Another way to denote vectors is in terms of the standard unit vectors denoted $\vc{i}$ and $\vc{j}$. A unit vector is a vector whose length is one. The vector $\vc{i}$ is the unit vector in the direction of the positive $x$-axis. In coordinates, we can write $\vc{i}=(1, 0)$. Similarly, the vector $\vc{j}$ is the unit vector in the direction of the positive $y$-axis: $\vc{j}=(0, 1)$. We can write any two-dimensional vector in terms of these unit vectors as $\vc{a}=(a_1, a_2) = a_1\vc{i}+a_2\vc{j}$.