Orders of magnitude (numbers)

As noted above, one of the most elusive, but important skills is to be able to quickly and efficiently estimate the orders of magnitude associated with some quantity of interest. Earlier, we provided some of the conceptual rules that fuel such estimates. Here, we complement those conceptual rules with various helpful numerical rules that can be used to quickly find our way to an approximate but satisfactory assessment of some biological process of interest. We do not expect you to remember them all on first pass, but give them a quick look and maybe a few of them will stick in the back of your mind when you need them.

Arithmetic sleights of hand

• 210 ≈1000
• 220 = 410 ≈106
• e7 ≈103
• 100.1 ≈1.3
• √2 ≈1.4
• √0.5 ≈0.7
• ln(10) ≈2.3
• ln(2) ≈0.7
• log10(2) ≈0.3
• log10(3) ≈0.5
• log2(10) ≈3

Big numbers at your disposal

• Seconds in a year ≈π x107 (yes, pi, just a nice coincidence and easy way to remember)
• Seconds in a day ≈ 105
• Hours in a year ≈ 104
• Avogadro’s constant ≈ 6×1023
• Cells in the human body ≈ 4×1013

Rules of thumb

Just as there are certain arithmetical rules that help us quickly get to our order-of-magnitude estimates, there are also physical rules of thumb that can similarly extend our powers of estimation. We give here some of our favorites and you are most welcome to add your own at the bottom and also send them to us. Several of these estimates are represented pictorially as well. Note that here and throughout the book we try to follow the correct notation where “approximately” is indicated by the symbol ≈, and loosely means accurate to within a factor of 2 or so. The symbol ~ means “order of magnitude” so only to within a factor of 10 (or in a different context it means “proportional”). We usually write approximately because we know the property value indeed roughly but to better than a factor of 10 so ≈ is the correct notation and not ~. In the cases where we only know the order of magnitude we will write the value only as an exponent 10x without extraneous significant digits.

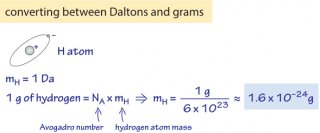
• 1 Dalton = 1 g/mol ≈ 1.7×10-24 g (as derived in Figure 1)
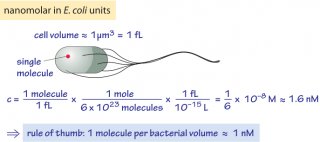
• 1 nM is about 1 molecule per bacterial volume as derived in Figure 2, 101-102 per yeast cell and 103-104 molecules per characteristic mammalian (HeLa) cell volume. For 1 µM multiply by a thousand, for 1 mM multiply by a million.
• 1 M is about one per 1 nm3
• There are 2-4 million proteins per 1 nm3 of cell volume
• Concentration of 1 ppm (part per million) of the cell proteome is ≈ 5 nM.
• 1 µg of DNA fragments 1 kb long is ≈1pmol or ≈1012 molecules
• Under standard conditions, particles at a concentration of 1M are ≈1 nm apart
• Mass of typical amino acid ≈100 Da
• Protein mass [Da] ≈100 x Number of amino acids
• Density of air ≈1 kg/m3
• Water density ≈55 M ≈ x 1000 that of air ≈1000 kg/m3
• 50 mM osmolites ≈1 Atm osmotic pressure (as shown in Figure 3)
• A base pair has a volume of ≈1 nm3
• A base pair has a mass of ≈600 Da
• Lipid molecules have a mass of ≈500 -1000 Da
• 50 mM osmolites ≈1 Atm osmotic pressure
• Water molecule volume ≈0.03 nm3, (≈0.3 nm)3
• 1 kBT ≈ 2.5 kJ/mol ≈ 0.6 kcal/mol ≈ 25 meV ≈ 4 pN nm ≈ 4×10-21 J
• ≈6 kJ/mol sustains one order of magnitude concentration difference (=RT ln(10) ≈ 1.4 kcal/mol)
• Movement across the membrane is associated with 10-20 kJ/mol per one net charge due to membrane potential
• ATP hydrolysis under physiological conditions releases 20 kBT ≈ 50 kJ/mol ≈ 12 kcal/mol ≈ 10-19 J
• One liter of oxygen releases ≈20 kJ during respiration
• A small metabolite diffuses 1 nm in ~1 ns
• 1 OD600 ≈0.5 g cell dry weight per liter
• ≈1010 carbon atoms in a 1 mm3 cell volume